Let's Calculate Bach - Applying Information Theory and Statistics to Numbers in Music
Extract from the Introduction:
On a student exchange with Germany I happened to read a book in the local library which must have been "Johann Sebastian Bach bei seinem Namen gerufen: eine Noteninschrift und ihre Deutung." Smend, Friedrich. Bärenreiter, Kassel 1950 and this piqued my interest in the subject of numerology. But pursuit of musical interests took a back seat to my family and my working life in programming real-time operating systems and industrial process control systems, and then in IT service management and IT governance. In the meantime, much more has been written about numbers in Bach, and the use of personal computers has opened up new avenues of enquiry, which I have not seen pursued in the literature so far. During my final working years I was investigating the application of risk management to IT and learned some things about statistics, the pitfalls of dealing with probabilities and cognitive biases. I hope that this combination of information theory, computer technology, probability and statistics, cognitive psychology and music, supplemented by a computer program provided to assist in exploring certain aspects, can add some new perspectives and provide additional support for future musicological research.
More information:
Click on the book cover to go to the Springer website, where you can view the table of contents and abstracts of all the chapters and download the front matter and back matter.
More information:
Click on the book cover to go to the Springer website, where you can view the table of contents and abstracts of all the chapters and download the front matter and back matter.
Reviews:
Robert L. Wells, University of Mary WashingtonBACH: Journal of the Riemenschneider Bach Institute, Vol. 54, No. 1, 2023
Program
The computer program, called "Proportional Parallelism Explorer", is intended to find proportions in the lengths of pieces in collections of music. It was used to obtain the results described in chapters 8-10 of the above book, which investigate the concept introduced inRuth Tatlow, Bach's Numbers - Compositional Proportion and Significance, Cambridge University Press 2007.
Main Features
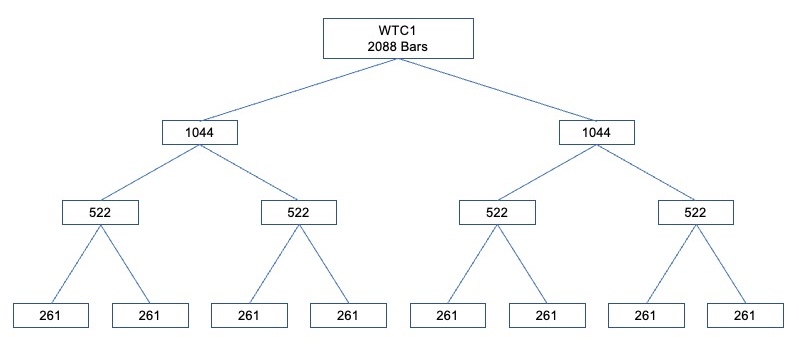
Dividing the 2088 bars of J.S. Bach's Well Tempered Clavier Book 1 into layers of 1:1 Proportion
- Take an input file with a list of pieces, each with a name and number (e.g. the length of the piece).
- Find all combinations of separating the pieces into two sets that will add up to a given proportion 1:1, 1:2, 2:3, etc.
- Search for patterns of how the pieces are distributed between the two sets, e.g. the first half against the second half, the even ones against the odd, etc.
- Carry this procedure into further layers to find the proportions in subsets of the two initial sets.
- Perform Monte Carlo Simulations to see how the given numbers compare with equivalent sets of random numbers.
- The output is to CSV files suitable for reading in Excel®, including summary data.
Additionally, the manual can be viewed here.